You have to determine the equation, in slope-intercept form, of the perpendicular bisector of the line segment with endpoints (5,8) and (-3,12)
The line you have to determine is a bisector of the given line segment, which means that intersects the line segment at its midpoint.
First, let's determine the coordinates of the midpoint between (5,8) and (-3,12).
I will consider:
(x₁,y₁) = (-3,12)
(x₂,y₂) = (5,8)
x-coordinate of the midpoint (xM)
-First, calculate the difference between the x-coordinates of both endpoints
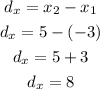
-Second, subtract half the difference to x₂ to determine the x-coordinate of the midpoint (M).
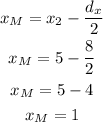
y-coordinate of the midpoint (yM)
-First, calculate the difference between the y-coordinates of both endpoints
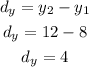
-Second, add half the difference to y₂
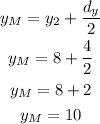
The coordinates of the midpoint are M(1,10)
Next, we have to determine the slope of the perpendicular line.
If two lines are perpendicular, then their slopes are reverse opposites, let "m" and "n" represent the slopes of two perpendicular lines, you can express their relationship as:

Using the formula for the slope and the coordinates of both endpoints, you can determine the slope of the given line segment.
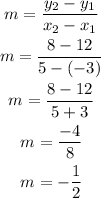
The slope of the line segment is m=-1/2, the slope of a line perpendicular to this line segment will be the inverse opposite:
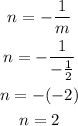
The slope of the perpendicular line is n=2
We have determined that the perpendicular bisector of the segment between (5,8) and(-3,12) has a slope of n=2 and passes through the point M (1,10), using the point-slope form you can determine the equation of the said line:

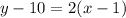
-Distribute the multiplication on the parentheses term:
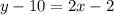
-Add 10 to both sides of the equal sign:
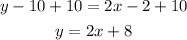
The equation in the slope-intersect form of the perpendicular bisector of the line segment between (5,8) and (-3,12) is y = 2x + 8
You can graph this line and the line segment: