Answer:
208.02 m
Explanation:
When the model rocket lands, y = 0; therefore, the equation becomes

Using the quadratic formula we solve for x.
![x=\frac{-8.3\pm\sqrt[]{8.3^2-4(-0.04)(4.3)}}{2(-0.04)}](https://img.qammunity.org/2023/formulas/mathematics/college/aq3wmsvzrypj5ytj4o1stqg1yxhtkvazbo.png)
Which simplifies to give
![x=\frac{-8.3\pm\sqrt[]{69.578}}{(-0.08)}](https://img.qammunity.org/2023/formulas/mathematics/college/qs8c9f5sihuiyetnp056h1xb4m0r53y91h.png)
Hence, we have the solutions
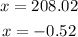
since lengths cannot be negative, we choose x = 208.02 as our answer.
Hence, the model rocket lands 208.02 m from the starting point.