Consider the next polynomial function,

Notice that f(x) has one real zero and two complex zeros.
However, the expanded form of f(x) is
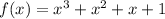
Therefore, f(x) is a polynomial of degree 3 with real coefficients that has exactly 1 real zero and 2 complex zeros.
This is a counterexample of the statement. The answer is False.