We have to find after how many months will the total amount of money paid to both gyms be the same and what will this amount be.
To find that we have to write a function that relates months to total cost for each gym.
For Community Gym, we have a fixed cost, the membership, of $50. This amount is independent of the months.
Then, it has a monthly fee of $60, so it will affect the total cost proportionally to the number of months: if n are the numbers of month, the total cost of this monthly fee will be 60n.
If we add the cost of the membership we get:
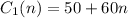
In the case of Workout Gym, the fixed cost (one-time membership) is $170 and the monthly fee is $50, so if n are the months, we can write the total cost as the sum of boths:
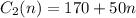
Now that we have the cost functions, we can find the months at which both gyms cost the same by writing:
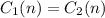
This equation tells us that both costs are the same, and this will happens for an specific number of months. We can find the number of months n as:
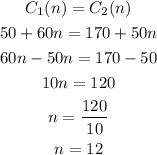
With this result (n=12), we know that both gyms will cost the same amount of money at 12 months.
We can calculate the amount of money by replacing n with 12 in any of the two equations:
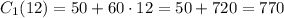
We can check with the other equation:
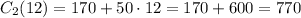
Answer: the number of months is 12 months. The amount of money is $770 for this period.