We can see a quadratic function, and we have that the leading term of the function is negative. This means that the quadratic function has a maximum. We need to remember that the axis of symmetry of a quadratic function of this form is a vertical line which formula is given by:

1. Then since we have that the quadratic function, in this case, is given by:
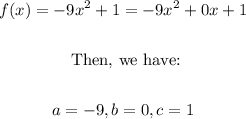
2. Now, we can apply the formula for the axis of symmetry as follows:
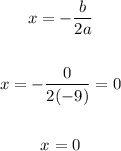
Therefore, in summary, the axis of symmetry is given by x = 0.