Question

A vector points -43.0 unitsalong the x-axis, and 11.1 unitsalong the y-axis.Find the direction of the vector.Y

Answer 1

The vector will be represent (not accurately) like the diagram below:

Now, from the expression

`\theta=\tan ^(-1)((v_x)/(v_y))`

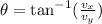
we get the pink angle, but we need the green angle. To get the correct one we calculate the pink one and then we find its supplementary angle; let's do that:

`\begin{gathered} \theta=\tan ^(-1)((11.1)/(43)) \\ \theta=14.47 \end{gathered}`

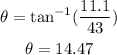
Now, the green angle will be:

`180-14.47=165.53`

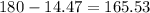
Therefore the direction of the vector is 165.53°