Question

Solve the following system using the elimination method. Enter your answer as an ordered pair in the form (x,y) if there is one, unique solution. Enter All if there are infinitely many solutions and enter None if there are no solutions. 6x-5y=392x+6y=-10

Answer 1

Given the system of equations:

`\begin{gathered} 6x-5y=39\rightarrow(1) \\ 2x+6y=-10\rightarrow(2) \end{gathered}`

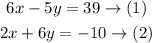
We will use the elimination method to find the solution to the system

We will eliminate (y) first, then solve the equations for (x)

Multiply the first equation by (6) and the second equation by (5) then add the new equations

The steps will be as follows:

`\begin{gathered} 6x-5y=39\rightarrow(*6) \\ 2x+6y=-10\rightarrow(*5) \\ ============== \\ 36x-30y=234 \\ 10x+30y=-50 \\ ============== \\ 46x=234-50 \\ 46x=184 \\ x=(184)/(46)=4 \end{gathered}`

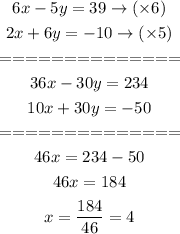
To find (y), substitute with (x) into equation (1)

`\begin{gathered} 6\cdot4-5y=39 \\ 24-5y=39 \\ -5y=39-24 \\ -5y=15 \\ y=(15)/(-5)=-3 \end{gathered}`

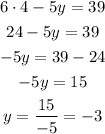
So, the answer will be:

`(x,y)=(4,-3)`