Question

You are choosing two cards from a standard deck of cards, without replacement. What is the probability of selecting a two and then an odd number card?

Answer 1

We will have the following:

We know that a standard deck of cards has 52 cards, composed of 4 sets, from which each set is composed of:

ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, jack, queen and king.

Now, the probability of getting a 2 is:

`p_1=(4)/(52)`

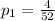
And the probability of getting an odd number card [assuming the ace counts as a 1] will be:

`p_2=(20)/(52)`

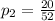
So, the probability of the evens happening one after the other is:

`\begin{gathered} p_3=p_1p_2\Rightarrow p_3=((4)/(52))((20)/(52)) \\ \\ \Rightarrow p_3=(5)/(169)\Rightarrow p_3=0.02958579882... \\ \\ \Rightarrow p_3\approx0.03 \end{gathered}`

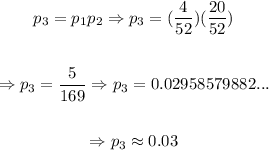
So, the probability is approximately 0.03.