Assume that the width of the frame is x, then
The length and the width of the picture with the frame will increase by 2x (x for each side), then
L = 6 + 2x
W = 4 + 2x
Since the total area is 80 in.^2, then

Substitute the values of L and W
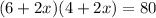
Now, we will solve the equation
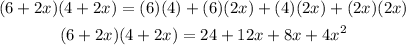
Add the like terms

Now, equate it by 80
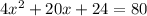
Subtract 80 from both sides

Divide all terms by 4 to simplify the equation
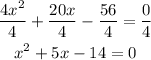
The equation is
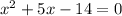
Now, factorize it into 2 factors
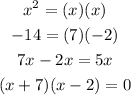
Equate each factor by 0 to find x
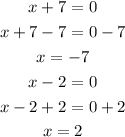
We will refuse x = -7 because the length must be a positive number, then
The width of the frame is 2 inches