Answer:
a. 56 meters
b. 89.7 meters
Step-by-step explanation:
Part A.
The distance from A to the foot of the pole is the segment AC.
First, we find the measure of angle ∠ BCA.
Since ∠ BCA is part of a triangle,
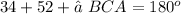
Solving for ∠ BCA gives

Next, we use the law of sines, which in our case says
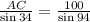
Solving for AC gives
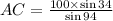
which we evaluate to get (rounded to the nearest whole number.
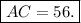
Part B.
The height of the pole is the length DC.
Let us first find the measure of the angel ∠ADC.
Since ∠ADC is the interior angle of a triangle,
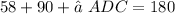
solving for ∠ADC gives
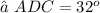
Now we use the law of sines again.
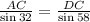
Since AC = 56, the above becomes
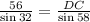
solving for DC gives
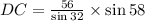
which evaluates to give (rounded to the nearest tenth)
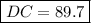
Hence, to summerise
a. 56 meters
b. 89.7 meters