Step 1 - Remembering the definition of concentration
The molar concentration of a solution is defined as the quotient between the number of moles of solute (n) and the total volume of solution (V):
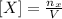
This equation can be read as the concentration of solute X equals its number of moles divided by the total volume of the solution.
Step 2 - Calculating the molarity of the given solution
We must discover the required number of moles of solute. We have the total volume of the solution (77.6ml) and its final concentration.
Let's substitute these in the formula:
![\begin{gathered} [urea\rbrack=(n_(urea))/(V) \\ 3.5=(n_(urea))/(0.0776) \\ \\ n_(urea)=3.5*0.0776=0.27\text{ moles} \end{gathered}]()
Answer: 0.27 mol would be needed