Question

Rose can choose between two summer jobs. She can work as a checker in a discount store for $8.40 an hour, or she can mow lawns for $12.00 an hour. In order to mow lawns, she must buy a $450 lawnmower. For how many hour must Rose work in order for the mowing to be more profitable than checking?

Answer 1

Explanation:

Step 1. We will define the variable 'x' as the number of hours worked.

Since she earns $8.4 per hour working at the store, her earnings from that job would b:

`8.4x`

we multiply the payment per hour 8.4 by the number of hours worked.

Step 2. Her earnings as a lawnmower would be $12.0 per hour multiplied by the number of hours 'x', but since here she needs to buy a $450 lawnmower, this will be deducted from her earnings:

`12x-450`

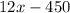
Step 3. For mowing lawns to be more profitable than working as a checker at the store, her earnings at the two jobs must be equal for a certain value of x:

`12x-450=8.4x`

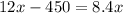
Step 4. Solving the equation for x:

`\begin{gathered} 12x-8.4x=450 \\ \downarrow \\ 3.6x=450 \end{gathered}`

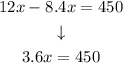
Dividing both sides by 3.6

`\begin{gathered} x=450/3.6 \\ \downarrow \\ x=125 \end{gathered}`

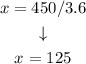
This means that if she works 125 hours, her earnings will be the same as a checker and as a lawnmower, therefore, she just needs to work one more hour -- 126 hours (or more) for the mowing to be more profitable than checking.

The answer is at least 126 hours.

Answer: 126 hours