we have the function
![f(x)=\frac{x+1}{x\sqrt[]{x}}](https://img.qammunity.org/2023/formulas/mathematics/college/ybxligr2oej8bu3ykj6qwpw53tfd4qwcps.png)
Complete the table
Substitute each value of x in the given function to obtain the value of f(x0
so
For x=10^0=1
![f(x)=\frac{1+1}{1\sqrt[]{1}}=2](https://img.qammunity.org/2023/formulas/mathematics/college/f0jhbhu7leratf08s3joab6tea7yq1rqlv.png)
For x=10^1=10
![f(x)=\frac{10+1}{10\sqrt[]{10}}=0.348](https://img.qammunity.org/2023/formulas/mathematics/college/z80zkdimkf7e1ekuh0wlp0vaqnbyfhmbgd.png)
For x=10^2=100
![f(x)=\frac{100+1}{100\sqrt[]{100}}=0.101](https://img.qammunity.org/2023/formulas/mathematics/college/vsgqmbk6xwjpujnt10jz2al40zeef0mizo.png)
For x=10^3=1,000
![f(x)=\frac{1000+1}{1000\sqrt[]{1000}}=0.032](https://img.qammunity.org/2023/formulas/mathematics/college/xhhb8kz51ooh3ff7a6dh0q74rps7dqt4ed.png)
For x=10^4=10,000
![f(x)=\frac{10000+1}{10000\sqrt[]{10000}}=0.010](https://img.qammunity.org/2023/formulas/mathematics/college/zqjz80wtyvxwfqkgmgy8p0yn7fpz0z4j04.png)
For x=10^5=100,000
![f(x)=\frac{100000+1}{100000\sqrt[]{100000}}=0.003](https://img.qammunity.org/2023/formulas/mathematics/college/avgn6j0nkqwzr1r2fcglvft5rulx7jn6uy.png)
For x=10^6=1,000,000
![f(x)=\frac{1000000+1}{1000000\sqrt[]{1000000}}=0.001](https://img.qammunity.org/2023/formulas/mathematics/college/nn402oe45j0e3i504ar5r0tlp1oht396pr.png)
therefore
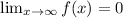
see the attached figure below
as the value of x increases -----> the value of f(x) decreases
as x ----> ∞ f(x) ---> 0