Question

A number n, is added to 15 less than 3 time itself. The result is 101. Which equation can be used to find the value of n? 3n-15+n=101 3n+15+n=1013n-15-n=1013n+15-n=101

Answer 1

As given by the question

There are given that the a number is n

Now,

According to the given statement:

Number n is added to 15

That means:

`15+n`

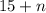
Then,

Number n is added to 15 less than 3 times itself and the result is 101.

That means:

`3n-15+n=101`

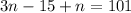
Hence, the correct option is A