Using the circle theorem for the intersection of a tangent and a chord:
An angle formed by a chord and a tangent that intersect on a circle is half the measure of the intercepted arc.
Using the theorem, we can write:
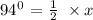
Solving for x:
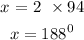
Similarly, we can write:
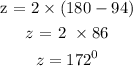
Answer:
z = 172 degrees