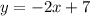We can get the equation of the line by using the Point-Slope Formula.
The Point-Slope Formula is used when we have one point on the line that isn't the y-intercept and the slope. It is given as:

where:
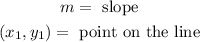
Parameters:
The point is given in the question to be:
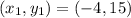
The slope: We are given that the line is parallel to the line
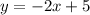
Comparing with the Slope-Intercept form of a straight line given as:

where m is the slope, we have the slope of the line to be:
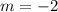
Formula:
We can now input these into the formula and we get the equation below:

Hence, we can rewrite the equation to be:

The answer is: