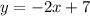Question

HelpppWhat is the equation of the line that goes through the point (-4, 15) and is parallel to theequation y = –2x + 5?

Answer 1

We can get the equation of the line by using the Point-Slope Formula.

The Point-Slope Formula is used when we have one point on the line that isn't the y-intercept and the slope. It is given as:

`y-y_1=m(x-x_1)`

where:

`\begin{gathered} m=\text{ slope} \\ (x_1,y_1)=\text{ point on the line} \end{gathered}`

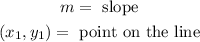
Parameters:

The point is given in the question to be:

`(x_1,y_1)=(-4,15)`

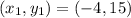
The slope: We are given that the line is parallel to the line

`y=-2x+5`

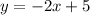
Comparing with the Slope-Intercept form of a straight line given as:

`y=mx+b`

where m is the slope, we have the slope of the line to be:

`m=-2`

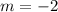
Formula:

We can now input these into the formula and we get the equation below:

`\begin{gathered} y-15=-2(x-\lbrack-4\rbrack) \\ y-15=-2(x+4) \end{gathered}`

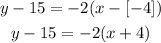
Hence, we can rewrite the equation to be:

`\begin{gathered} y-15=-2x-8 \\ y=-2x-8+15 \\ y=-2x+7 \end{gathered}`

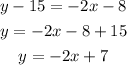
The answer is:

`y=-2x+7`