We are given a right-angled triangle.
With respect to angle 49°, the adjacent side is 11 and the opposite side is x
Recall from the trigonometric ratios,
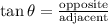
For the given case, we have
θ = 49°
Opposite = x
Adjacent = 11
Let us substitute these values into the above formula
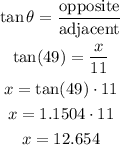
Therefore, the value of x is 12.654
The last option is the correct answer.