Starting with the expression:
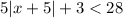
substract 3 from both sides of the inequality:
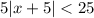
divide both sides by 5:
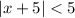
There are two cases.
Case 1: x+5 is greater or equal to 0.
In this case, |x+5| = x+5, then:
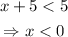
Since by hypothesis:
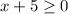
then also:
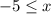
Then, for case 1, we have that:

Case 2: x+5 is lower than 0
In this case, |x+5|=-x-5, then:
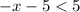
add x-5 to both sides:
[tex]\begin{gathered} -x-5+x-5<5+x-5 \\ \Rightarrow-10Since x+5 is lower than 0, then: