1 Answer

Vishnuprasad R · Answer 1 · 2023-12-16T05:51:18+0000

Given the shown frequency distribution table.

We will find the following:

N = the total frequency = 2 + 2 + 3 + 5 + 2 = 14

b.

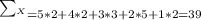
$\sum_^X=5*2+4*2+3*3+2*5+1*2=39$

C.

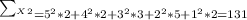
$\sum_^X^2=5^2*2+4^2*2+3^2*3+2^2*5+1^2*2=131$

D. Sum of Squares has the following formula:

$SS=\sum_^X^2-\frac{(\operatorname{\sum}_^X)^2}{N}$

Substitute from a, b, and c

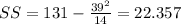
So, the answer will be:

a. N = 14

b. ∑X = 39

c. ∑X² = 131

d. SS = 22.36

Please log in or register to add a comment.