Question

Determine the altitude necessary to establish a circular geostationary orbit about a planet with the following characteristics: mass = 5 x10²⁶ kg; radius = 9 x 10⁶ m 1 day = 2 x 10⁴ seconds. Express result in km.

Answer 1

60.65 x 10³ km

Step-by-step explanation

We know that 1 day - which is 1 complete turn of the planet, is equivalent to 2x10⁴ seconds. This means that the angular velocity of the planet is,

`\omega=(1)/(2*10^4s)=5*10^(-5)\text{turns per second}`

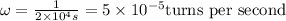
If the orbit is geostationary, the object in orbit will have a fixed position related to the planet. Thus, this object will have the same angular velocity as the planet.

Let's say that the object in orbit has mass m, while the planet's mass is M. Let's draw a diagram of the situation,

Because of the object's rotational motion, the net force acting on the object in orbit is,

`F_(net)=m\cdot a_c=m\cdot(\omega^2\cdot(R+h))`

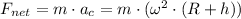
This is the result of the gravitational force of the planet and the object in orbit,

`F_(grav)=G\cdot(M\cdot m)/((R+h)^2)`

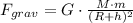
Note that (R + h) is the orbital radius, but we are only interested in the altitude, which is the distance from the surface of the planet to the orbit.

As stated before, these two forces are equal in magnitude,

`m\cdot\omega^2\cdot(R+h)=G\cdot(M\cdot m)/((R+h)^2)`

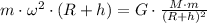
We have to solve this equation for h. First, the mass of the object in orbit, m, cancels out,

`\omega^2\cdot(R+h)=G\cdot(M)/((R+h)^2)`

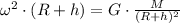
Next, we have to multiply both sides by (R+h)²,

`\begin{gathered} \omega^2\cdot(R+h)\cdot(R+h)^2=G\cdot(M)/((R+h)^2)\cdot(R+h)^2 \\ \\ \omega^2\cdot(R+h)^3=G\cdot M \end{gathered}`

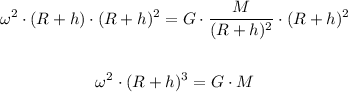
Divide both sides by ω²,

`\begin{gathered} (\omega^2\cdot(R+h)^3)/(\omega^2)=(G\cdot M)/(\omega^2) \\ \\ (R+h)^3=(G\cdot M)/(\omega^2) \end{gathered}`

Take the cubic root of both sides and subtract R from both sides - in that order,

`h=\sqrt[3]{(G\cdot M)/(\omega^2)}-R`

This is the altitude of the orbit. The symbols in this equation are:

• G is the gravitational constant, 6.67 x 10⁻¹¹ N*m²/kg²

,

• M is the mass of the planet, 5 x 10²⁶ kg

,

• R is the radius of the planet, 9 x 10⁶ m

,

• ω is the angular velocity of the planet - and the object, we found before, 5 x 10⁻⁵ turns per second.

Before solving the equation, we have to write the angular velocity in radians per second, knowing that 1 turn is equivalent to 2π radians,

`\omega=5*10^(-5)(turn)/(s)\cdot\frac{2\pi\text{rad}}{1\text{ }turn}=10\pi*10^(-5)rad/s`

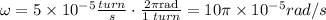
The altitude is,

`h=\sqrt[3]{(6.67*10^(-11)N\cdot m^2/kg^2\cdot5*10^(26)kg)/((10\pi*10^(-5)rad/s)^2)}-9*10^6m\approx60.65*10^6m=60.65*10^3km`

Hence, the altitude of the geostationary orbit should be 60.65 x 10³ km.