Let's take a look at our triangle:
Now, using the law of sines, we'll get that:
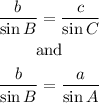
We know that the sum of the three interior angles of a trianlge is 180°. Therefore, we can conclude that:
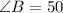
Now. solving for a and c,
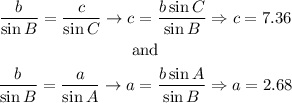
This way, we know the lenght of the three sides of the triangle:
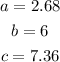
Now, we can calculate the area of such triangle using Heron's formula:
![A=\sqrt[]{s(s-a)(s-b)(s-c)}](https://img.qammunity.org/2023/formulas/mathematics/college/t3rmhsk71nltcmgtu237bvtgrmrx89v4xv.png)
Where:
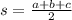
Using this, and the sides we've just calculated, we'll have that:
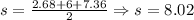
Thereby,
![\begin{gathered} A=\sqrt[]{8.02(8.02-2.68)(8.02-6)(8.02-7.36)} \\ \Rightarrow A=7.56 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6wfnj0l3ngcni3wj0fls3fwbgi98b3hzwi.png)
We can conclude that the area of the triangle is 7.56 square feet