The equation in the table is linear because as the x values increase by 1, and y values increase by 3.
The general form of a linear equation is :
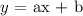
where:
a is the slope and b is the intercept
The slope can be calculated using the fomula:
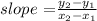
where (x1,y1) and (x2,y2) are two points on the table.
We can find two points on the table:
(6, 13) and (7, 16)
Hence, the slope:
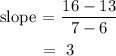
The intercept is the value of y when the line cuts the y-axis.
Using the formula for slope and the point (0,y), we can find the intercept.
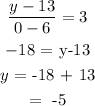
Hence, the required equation is:
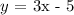
Answer:
y = 3x - 5