Given:
Dimeter of the circle is d.
As circle lies inside the square. So, the length of the side of square is also d units.
The area of the circle is given as,

Now, the area of the square is,
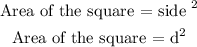
To find the area of paper that wasted when the circle is cut out of the square,

Answer: option D) is correct.