SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the formula for finding the perimeter of the fence

STEP 2: Write the dimensions of the Fence

Hence, the width will result in the greatest possible area of the dog pen is:

STEP 3: Calculate the greatest possible area of the dog pen
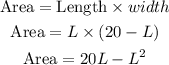
STEP 4: Calculate the length will result in the greatest possible area of the dog pen
![undefined]()