Question

Let x be a continuous random variable that is normally distributed with a mean of 136.4 and a standard deviation of 18.5. Find the probability that x assumes a value between 109.1 and 130.5.Round your answer to four decimal places.The probability = Enter your answer in accordance to the question statement

Answer 1

Probability that x assumes a value between 109.1 and 130.5:

`z=(109.1-136.4)/(18.5)=(-27.3)/(18.5)=-1.47`

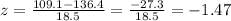
Using a z-score table find the corresponding value for z=-1.47:

2. Find the z-score for P(x<130.5)

`z=(130.5-136.4)/(18.5)=(-5.9)/(18.5)=-0.32`

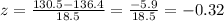
3. Subtract the z-score of upper limit by the z-score of lower limit:

`0.3745-0.0708=0.3037`

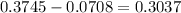
Then, the probability that x assumes a value between 109.1 and 130.5 is:

[tex]P(109.1