Question

7x + 3y = 5 find the slope and y intercept and make a new equation find if there’s one solution no solution or an infinite number of solutions 4x + 3y =6 the slope and y intercept and make a new equation find if there’s one solution no solution or an infinite number of solutions

Answer 1

Hello there. To solve this question, we'll have to remember some properties about system of linear equations and how to find the equation of a line in slope-intercept form.

Given the equation of a line

`ax+dy=c`

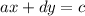
We can solve for y in order to find it in slope-intercept form

`y=mx+b`

Where m is the slope and b is the y-intercept.

For the first equation, we get

`7x+3y=5`

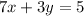
Solving for y, we first subtract 7x on both sides of the equation

`3y=-7x+5_{}`

Divide both sides of the equation by a factor of 3

`y=-(7)/(3)x+(5)/(3)`

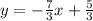
And we can spot the slope as m = -7/3 and the y-intercept = 5/3.

For the second equation, we have

`4x+3y=6`

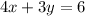
Solving for y, subtract 4x on both sides of the equation

`3y=-4x+6`

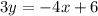
Divide both sides by a factor of 6

`y=-(4)/(3)x+2`

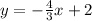
The slope in this case is equal to -4/3 and the y-intercept is equal to 2.

Finally, to determine if the system has one, infinite or no solutions, we make:

`\begin{cases}7x+3y=5 \\ 4x+3y=6\end{cases}`

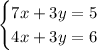
The first way to make sure is that if we can find a single ordered pair (x, y) that satisfies this system. Subtract the second equation from the first, such that

`\begin{gathered} 7x+3y-(4x+3y)=5-6 \\ 7x+3y-4x-3y=-1 \\ 3x=-1 \end{gathered}`

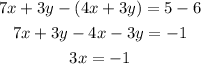
Divide both sides by a factor of 3

`x=-(1)/(3)`

Plugging this into any equation, we find the solution for y

`\begin{gathered} 4\cdot\mleft(-(1)/(3)\mright)+3y=6 \\ -(4)/(3)+3y=6 \\ 3y=6+(4)/(3)=(22)/(3) \\ y=(22)/(9) \end{gathered}`

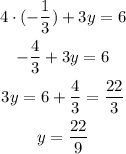
Hence the ordered pair that is a solution of this system of equations is

`\mleft(-(1)/(3),(22)/(9)\mright)`

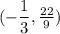
This is in fact the unique solution to this system, since the lines only cross this time at x = -1/3 and y = 22/9.

The other way to check is if the determinant of the coefficients matrix is different of zero:

`\begin{bmatrix}{7} & {3} \\ {4} & {3}\end{bmatrix}`

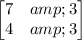
Taking this determinant, that is, subtracting the products between the main and secondary diagonals, we have

`7\cdot3-4\cdot3=21-12=9`

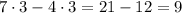
That means that this system has only one solution.

For a system of linear equations (in fact, two lines)