Take into account that the general equation of a line can be written as follow:
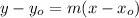
where m is the slope of the line and (xo,yo) are the coordinates of any point of the line.
In this case, you have:
m = -3
(xo,yo) = (-2,11)
Replace the previous values of the parameters into the general equation of the line and solve for y, as follow:
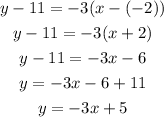
Hence, the equation of the line is y = -3x + 5