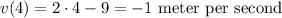Question

The displacement (in meters) of a particle moving in a straight line is given by s=t^2- 9t+ 15,(1) Find the average velocity over the time interval [3.5,4].Average Velocity ____meters per second.(in) Find the average velocity over the time interval [4,5].Average Velocity ___meters per second (iv) Find the average velocity over the time interval [4,4.5].Average Velocity ____meters per second.(B) Find the instantaneous velocity when t = 4Instantaneous velocity= ____meters per second

Answer 1

The displacement (in meters) of a particle moving in a straight line is given by:

`s(t)=t^2-9t+15`

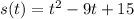
The average velocity is defined as the division between the displacement and the time:

`v_{\text{average}}=(\Delta s)/(\Delta t)`

(1)

For the time interval [3.5, 4]:

`\begin{gathered} \Delta t=4-3.5=0.5 \\ s(3.5)=3.5^2-9\cdot3.5+15=-4.25 \\ s(4)=4^2-9\cdot4+15=-5 \\ \Rightarrow\Delta s=s(4)-s(3.5)=-0.75 \end{gathered}`

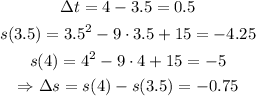
Now, using the equation for the average velocity:

`v_{\text{average}}=(-0.75)/(0.5)=-1.5\text{ meters per second}`

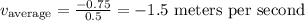
(2)

For the time interval [4, 5]:

`\begin{gathered} \Delta t=5-4=1 \\ s(5)=5^2-9\cdot5+15=-5 \\ s(4)=4^2-9\cdot4+15=-5 \\ \Rightarrow\Delta s=s(5)-s(4)=0 \end{gathered}`

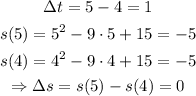
Now, using the equation for the average velocity:

`v_{\text{average}}=(0)/(1)=0\text{ meters per second}`

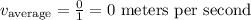
(3)

For the time interval [4, 4.5]:

`\begin{gathered} \Delta t=4.5-4=0.5 \\ s(4.5)=4.5^2-9\cdot4.5+15=-5.25 \\ s(4)=4^2-9\cdot4+15=-5 \\ \Rightarrow\Delta s=s(4.5)-s(4)=-0.25 \end{gathered}`

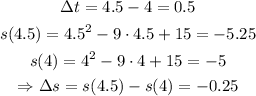
Now, using the equation for the average velocity:

`v_{\text{average}}=(-0.25)/(0.5)=-0.5\text{ meters per second}`

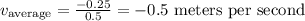
(4)

For the instantaneous velocity, given the displacement equation, we have:

`v(t)=2t-9`

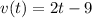
Now, for t = 4:

`v(4)=2\cdot4-9=-1\text{ meter per second}`