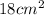First, calculate the surface area of each figure and then compare them.
Cube:
The cube is made up from 6 equal square surfaces. Then, the surface area is six time the area of one square. The area of each square is 9 squared cm, since:
![A=l^2=(3\operatorname{cm})^2=9cm^2]()
Then, the surface area of the cube is:
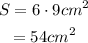
Rectangular prism
The rectangular prism has 6 faces, which are 3 pairs of rectangles.
Find the area of each type of rectangle. Then, add them twice to find the surface of the prism:
The first type of rectangle has sides of 3cm and 2cm. Then, the area is equal to:
![(3\operatorname{cm})(2\operatorname{cm})=6cm^2]()
The second type of rectangle has sides of 3cm and 6cm. Then, the area is equal to:
![(3\operatorname{cm})(6\operatorname{cm})=18cm^2]()
The third type of rectangle has sides of 2cm and 6cm. Then, the area is equal to:
![(2\operatorname{cm})(6\operatorname{cm})=12cm^2]()
Then, the total surface area of the prism is:
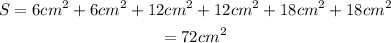
Finally, substract the area of the cube from the area of the rectangular prism to find how much greater the area of the prism is:
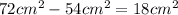
Therefore, the answer is: