Since line DB is perpendicular to line AC, then arc AB = arc BC
Thus, 14x - 3 = 7x + 18
Collecting like terms,
14x - 7x = 18 + 3
7x = 21
Dividing both sides by 7, we have
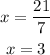
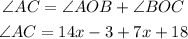
substituting x into the above equation,
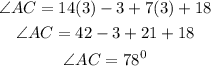
Hence, angle the arc AC makes at the centre is 78 degrees.