Question

30 cm 12 cm 18 cm Which is the best estimate of the figure in square centimeters?

Answer 1

Step-by-step explanation

Given:

A figure based on a right triangle, a rectangle, and a semicircle.

To determine the best estimate of the figure in square centimeters, we use areas of the figures as shown below:

For right triangle:

The formula of the area is:

`A=(bh)/(2)`

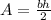
where:

b=base=12cm

h=height=12cm

A=Area

We plug in what we know:

`\begin{gathered} A=(bh)/(2) \\ =((12)(12))/(2) \\ Simplify \\ A=72cm^2 \end{gathered}`

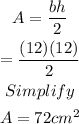
Hence, the area of the right triangle is 72 cm^2.

Next, we find for the area of the rectangle:

We use the formula:

`A=wl`

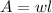
where:

w=width=12 cm

l=length = 18 cm

So,

`\begin{gathered} A=wl \\ =(12)(18) \\ Simplify \\ A=216cm^2 \end{gathered}`

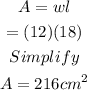
Hence, the area of the rectangle is 216 cm^2.

We also find the area of the semicircle using the formula:

`A=(\pi r^2)/(2)`

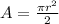
where:

r=radius = 12/2= 6cm

So,

`\begin{gathered} A=(\pi r^(2))/(2) \\ =(\pi(6)^2)/(2) \\ A=56.55cm^2 \end{gathered}`

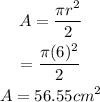
Hence, the area of the semicircle is 56.55 cm^2.

Then, we get the total:

Total =Area of the right triangle + Area of the rectangle+ Area of the semicircle

We plug in the values:

`\begin{gathered} Total\text{ Area = 72+216+56.55} \\ Calculate \\ Total\text{ Area=344.55 cm\textasciicircum2} \end{gathered}`

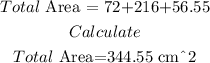
Therefore, the best estimate of the figure is 344.55 square centimeters.