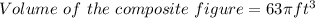Step-by-step explanation:
Given;
We are given a half sphere placed inside a cylinder.
The dimensions of both solid shapes are as follows;
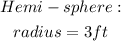
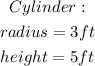
The volume of a hemisphere is given by the formula;
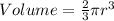
We shall substitute the values given and we'll have;
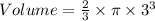
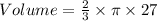
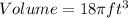
The volume of a cylinder is given by the formula;
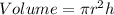
We now have;
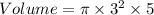
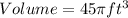
Therefore, the volume of the composite figure is;
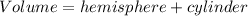
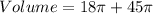
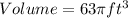
ANSWER: