Hello there. To solve this question, we'll have to remember some properties about investments.
Knowing Brent borrowed $2000 from his brother and will pay him the same amount of interest that he would have received if the money had been invested at 2.75% compounded quarterly, we need to find how much money will Brent repay his brother.
First, we have to remember the formula to find the amount a principal value P will become after t years, invested at an interesting rate r, compounded quarterly.
It is given by:
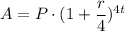
Plugging in P = 2000, r = 2.75% (converted in decimals, divide by 100) and t = 3, we get:

Add the values inside parenthesis and calculate the power (with the help of a calculator)
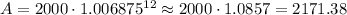
This is the amount Brent had to repay his brother.