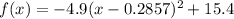Question

Part 1 - ApplicationPhysics shows that when an object is thrown upward with an initial velocity of v then its approximate height is given by this quadratic function.s = − 4. 9t^2+ 2.8t + 15I need help putting this into vertex form by completing the square.

Answer 1

Step-by-step explanation

Since we need to find the vertex of the parabola, we first should calculate the params (h,k), as shown as follows:

`h=-(b)/(2a)\text{ k=f(h)}`

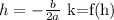
As the general form is as follows:

`f(x)=ax^2+bx+c`

We have that a=-4.9, b=2.8 and c=15

Computing the value of h:

`h=-(2.8)/(2\cdot(-4.9))`

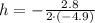
Multiplying numbers:

`h=(2.8)/(9.8)=0.28571\ldots`

Now, we need to compute the value of k:

`k=-4.9\cdot\: 0.28571\ldots^2+2.8\cdot\: 0.28571\ldots+15`

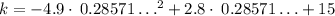
Multiplying numbers:

`=-0.28571\ldots^2\cdot\: 4.9+0.8+15`

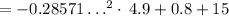
Adding numbers:

`=15.8-0.28571\ldots^2\cdot\: 4.9`
`=15.8-0.4`
`\mathrm{Subtract\: the\: numbers\colon}\: 15.8-0.4=15.4`
`=15.4`
`k=15.4`

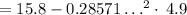
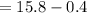
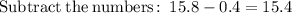
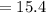
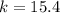
Therefore, the parabola vertex is (h,k) = (0.2857,15.4)

Thus, the equation of the parabola in vertex form is as follows:

`f(x)=-4.9(x-0.2857)^2+15.4`