Question

What is the maximum wavelength of light needed to eject electrons from a metal whose work function is 4.48 eV? What is the frequency of the light?

Answer 1

Given,

The work function of the metal, W=4.48 eV

The work function is given by the formula,

`W=h\upsilon_0`

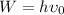
Where ν₀ is the threshold frequency of the metal.

But the frequency is related to wavelength as,

`\upsilon=(c)/(\lambda)`

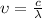
Where c is the speed of light and λ is the wavelength.

Thus the work function will be,

`W=(hc)/(\lambda_0)`

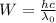
Where λ₀ is the maximum wavelength needed to eject the electron from the given metal.

On substituting the known values in the above equation,

`\begin{gathered} 4.48*1.6*10^(-19)\text{ J}=\frac{6.63*10^(-34)\text{ Js}*3*10^8\text{ m/s}}{\lambda_0} \\ \Rightarrow\lambda_0=\frac{6.63*10^(-34)\text{ Js}*3*10^8\text{ m/s}}{_{}4.48*1.6*10^(-19)\text{ J}} \\ =277.48*10^(-9)\text{ m} \end{gathered}`

Thus the maximum wavelength of the light required is 277.48 nm.

The frequency of the light is,

`\begin{gathered} \upsilon_0=(c)/(\lambda_0) \\ =(3*10^8)/(277.48*10^(-9)) \\ =1.08*10^(15)\text{ Hz} \end{gathered}`

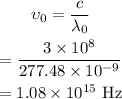
Thus the frequency of the required light is 1.08×10¹⁵ Hz.