Answer:
0.303 seconds
Step-by-step explanation:
We need to find the time that the cell phone takes to reach the sink. So, we will use the following equation
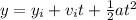
Where
yi is the initial position, so yi = 0.45 m
vi is the initial velocity. Since it is freefall, vi = 0 m/s
a is the acceleration due to gravity, so a = -9.8 m/s²
y is the final position, so y = 0 m
t is the variable that we need to find.
So, replacing the values, we get:
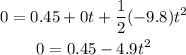
Now, we can solve for t
![\begin{gathered} -0.45=-4.9t^2 \\ (-0.45)/(-4.9)=t^2 \\ 0.09=t^2 \\ \sqrt[]{0.09}=t \\ 0.303\text{ s = t} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/high-school/fb9sxn2tlwxm7tv1oq74n0whirbx4344u6.png)
Therefore, you have 0.303 seconds before your cell phone is ruined.