Answer:
See the graph below
Step-by-step explanation:
Given:
Quadrilaterla EFGH on a coordinate plane
To find:
to graph the quadrilateral after a rotation of 90° counterclockwise around the origin.
The rule for a 90° counterclockwise around the origin is given as:
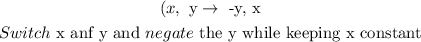
We will apply the rules to the coordinates of EFGH:
E = (3, 3)
F = (6, 3)
G = (6, 6)
H = (3, 6)
Applying the rule:
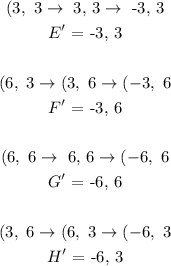
Plotting the graph: