We are given the following function:
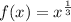
To determine the value of f(a) we will replace the value of "x" for "a" in the function:
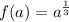
Using the same procedure we determine the value of f(b):

Now we determine the value of f(a+b):
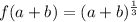
We are asked about the equatity:
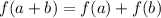
replacing the values we get:
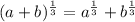
We get an equality that is not true for any value of "a" and "b" since the left expression can't be converted into the right expression for any "a" or "b". The statement is false.
The statement could be right if "a" or "b" equal zero, for example, let's take a = 0, we get:
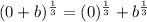
Simplifying:
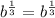
Which is a true statement. .