Question

2 A cognitive psychologist conducted a study of whether familiarity of words (X) predicts the time it takes (in seconds) to press a button indicating whether the word is singular or plural (I), with all participants being given the same words. Familiarity with these words was rated at a later time on a 7-point scale (with higher numbers indicating more farniliarity). The participants' scores were 6 2 5 3 7 Y 0.3 1.5 0.8 1.4 0.1 a Figure the Pearson correlation coefficient (25 pts.).

Answer 1

We will have the following:

*Firts: We have that the correlation coefficient is given by:

`r=\frac{\sum ^n_(i=1)X_iY_i-(1)/(n)(\sum ^n_(i=1)X_i)(\sum ^n_(i=1)Y_i)}{\sqrt[]{\sum^n_(i=1)X^2_i-(1)/(n)(\sum^n_(i=1)X_i)^2}\sqrt[]{\sum ^n_(i=1)Y^2_i-(1)/(n)(\sum ^n_(i=1)Y_i)^2}}`

*Second: We calculate the means, that is:

`x_m=4.6`

&

`y_m=\text{0}.82`

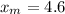
*Third: We calculate the sums:

`\sum ^n_(i=1)X^2_i-(1)/(n)(\sum ^n_(i=1)X_i)^2=123-(23^2)/(5)=17.2`
`\sum ^n_(i=1)Y^2_i-(1)/(n)(\sum ^n_(i=1)Y_i)^2=4.95-(4.1^2)/(5)=1.588`
`\sum ^n_(i=1)X_iY_i-(1)/(n)(\sum ^n_(i=1)X_i)(\sum ^n_(i=1)Y_i)=13.7-(23\cdot4.1)/(5)=-5.16`

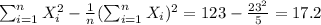
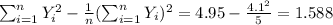
Fourth: We replace the data:

`r=\frac{-5.16}{\sqrt[]{17.2\cdot1.588}}\Rightarrow r=-0.987`

Thus making the coefficient r = -0.987.

And this would be the scatterplot: