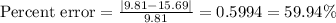Question

I need help filling out the acceleration for gravity due to the numbers in this chart

Answer 1

In order to calculate the acceleration of gravity, we can use the free fall formula:

`d=(gt^2)/(2)\to g=(2d)/(t^2)`

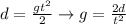
Where d is the distance travelled and t is the time.

So for each distance in the chart, we have:

`\begin{gathered} d=0.2\colon \\ g=(0.4)/(0.184^2)=11.81 \\ \\ d=0.4\colon \\ g=(0.8)/(0.258^2)=12.02 \\ \\ d=0.6\colon \\ g=(1.2)/(0.4^2)=7.5 \\ \\ d=0.8\colon \\ g=(1.6)/(0.236^2)=28.73 \\ \\ d=1\colon \\ g=(2)/(0.33^2)=18.37 \end{gathered}`

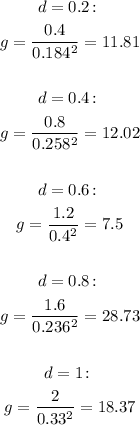
(All gravity units in m/s²)

Now, calculating the average, we have:

`g=(11.81+12.02+7.5+28.73+18.37)/(5)=15.69`

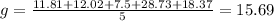
Finally, calculating the percent error, we have:

`\text{Percent error}=(|9.81-15.69|)/(9.81)=0.5994=59.94\text{\%}`