Given the coordinates of the following locations
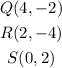
From the question we have that the distance of the point are equal so we will have;

Solving equation 1 and 3 simultaneously we will have
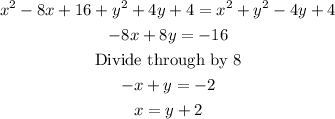
Solving equation 2 and 3 simultaneously we will have
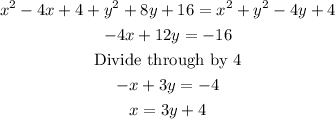
Thus , to solve for y we have;

Substitute y to find x
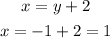
Hence the coordinates of the center of the merry-go-round is ( 1, - 1)
The second option is the correct option