SOLUTION
Given the equation as seen below, we can use the following steps to get the factors
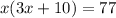
Step 1: Remove the bracket by multiplying the value outside the bracket with the one inside the bracket using the distributive law. We have:
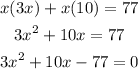
Step 2: Now that we have a quadratic equation, we solve for x using the quadratic formula:
![\begin{gathered} 3x^2+10x-77=0 \\ u\sin g\text{ the form }ax^2+bx+c=0 \\ a=3,b=10,c=-77 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ =\frac{-10\pm\sqrt[]{10^2-4(3)(-77)}}{2(3)} \\ =\frac{-10\pm\sqrt[]{100+924}}{6} \\ =\frac{-10\pm\sqrt[]{1024}}{6} \\ =(-10+32)/(6)\text{ or }(-10-32)/(6) \\ (22)/(6)\text{ or -}(42)/(6) \\ =(11)/(3)\text{ or }-7 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2dxspgc9c6imgg57usda3xnjrp8m3vjhd2.png)
Hence, it can be seen from above that the factors will be -7 or 11/3.