Completing squares
Before attempting to complete squares, let's recall the following identity
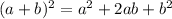
the expression at the right side can be converted to the square of a binomial, provided we have the terms completed as shown
We have the equation:
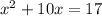
note the left side has TWO of the terms required for the square of a binomial. we only need the final number. but what number should we add?
the first term is the square of a, in this case, it's x
the second term has 10x and it should be 2ab, if we already know a=x, then
2ab=10x, then
b=10x/(2x)=5
now we know a=x and b=5, we only need to have b^2=25
that is exactly the number to add on both sides of the equation
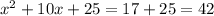
now we factor the left side:
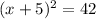
taking the square root, recall the square root can