11.
Given:
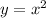
Differentiate with respect to x, we get
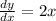
The given point is (3,9)
Substitute x=3 in the derivative, we get
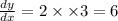
Hence the slope is 3.
12.
Given:
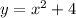
Differentiate with respect to x, we get
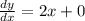
The given point is (0,4)
Substitute x=0 in the derivative, we get
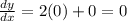
Hence the slope is 0.