Question

The value of China's exports of automobiles and parts (in billions of dollars) is approximately f ( x ) = 1.8208 e .3387 x , where x = 0 corresponds to 1998. In what year did/will the exports reach $7.4 billion?

Answer 1

We have the following equation:

`f(x)=108208e^(0.3387x)`

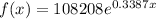
where x denotes the number of years after 1998.

By substituting the given information, we have that

`7.4=1.8208e^(0.3387x)`

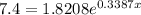
and we need to find x. Then, by dividing both sides by 1.8208, we get

`e^(0.3387x=)4.0641475`

then by taking natural logarithm to both sides, we obtain

`0.3387x=ln(4.0641476)`

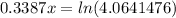
which gives

`0.3387x=1.4022040`

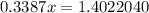
then, the number of years after 1998 is:

`\begin{gathered} x=(1.4022040)/(0.3387) \\ x=4.13996 \end{gathered}`

which means 4 years after 1998. Then, by rounding to the nearest year, the answer is 2002.