In order to determine the amount of tungsten after 147 days, use the following formula for the radioactive decay:
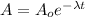
where
A: amount of tungsten after t days
Ao: initial amount of tungsten = 0.725 kg
t: time = 147 days
λ: decay constant
Then, it is necessary to find the value of λ. Use the following formula:
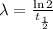
where t1/2 is the half-life of tungsten (69.4 days)
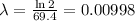
next, replace the previous result and the values of the other parameters into the formula for A:
![A=(0.725kg)e^(-(0.00998)(147))=(0.725kg)(0.23)=0.167\operatorname{kg}]()
Hence, after 147 days, there are 0.167 kg of tungsten 188