We have the following function
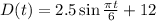
The maximum and minimum of that function happens when sin(x) = 1 or sin(x) = -1, respectively.
Then let's find the maximum, that happens when the sin value is 1
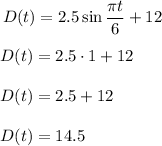
And the minimum, when sin value is -1
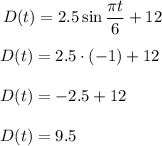
Then the least: 9.5 hours; greatest: 14.5 hours.