Question

Suppose 18 blackberry plants started growing in a yard. Absent constraint, the blackberry plants will spread by 85% a month. If the yard can only sustain 100 plants, use a logistic growth model to estimate the number of plants after 3 months.

Answer 1

The estimated number of plants after 3 months using the logistic model = 70 blackberry plants

Step-by-step explanation

If a population is growing in a constrained environment with carrying capacity K, and absent constraint would grow exponentially with growth rate r, then the population behavior can be described by the logistic growth model:

`P_n=P_(n-1)+r(1-(P_(n-1))/(K))P_(n-1)`

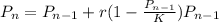
From the question,

`\begin{gathered} P_0=18,r=85\%=0.85,K=100 \\ \\ So, \\ \\ P_n=P_(n-1)=+0.85(1-(P_(n-1))/(100))P_(n-1) \end{gathered}`

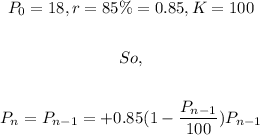
After the first month,

`\begin{gathered} P_(n-1)=P_0=18 \\ \\ \therefore P_1=P_0+0.85(1-(P_0)/(100))P_0 \\ \\ P_1=18+0.85(1-(18)/(100))18 \\ \\ P_1=18+0.85(1-0.18)18=18+0.85*0.82*18 \\ \\ P_1=18+12.546 \\ \\ P_1=30.546\text{ }plants \end{gathered}`

After the second month,

`\begin{gathered} P_1=30.546 \\ \\ \therefore P_2=P_1+0.85(1-(P_1)/(100))P_1 \\ \\ P_2=30.546+0.85(1-(30.546)/(100))30.546 \\ \\ P_2=30.546+0.85(1-0.30546)30.546=30.546+0.85*0.69454*30.546 \\ \\ P_2=30.546+18.033 \\ \\ P_2=48.579\text{ }plants \end{gathered}`

So after 3 months,

`\begin{gathered} P_2=48.579 \\ \\ \therefore P_3=P_2+0.85(1-(P_2)/(100))P_2 \\ \\ P_3=48.579+0.85(1-(48.579)/(100))48.579 \\ \\ P_3=48.579+0.85(1-0.48579)48.579=48.5796+0.85*0.5142*48.579 \\ \\ P_3=48.579+21.232 \\ \\ P_3=69.811\text{ }plants \\ \\ P_3\approx70\text{ }blackberry\text{ }plants \end{gathered}`

The estimated number of plants after 3 months using the logistic model = 70 blackberry plants.