Question

Find d and then find the 20th term the sequence. Type the value of d (just the number) in the first blank and then type the 20th term(just the number) in the second blank.a1=6 and a3=14

Answer 1

We have that an arithmetic sequence can be defined by the following explicit formula:

`a_n=a_1+(n-1)\cdot d`

where n represents the index of each term in the sequence and d represents the common difference beteen each term. a1 is the first term of the sequence.

In this case we have that the first term is a1 = 6, and also we have that a3=14. We can use the formula to find the common difference:

`\begin{gathered} a_3=a_1+(3-1)d \\ \Rightarrow a_3=a_1+2d \\ \Rightarrow14=6+2d \end{gathered}`

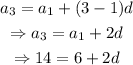
solving for d, we get:

`\begin{gathered} 2d+6=14 \\ \Rightarrow2d=14-6=8 \\ \Rightarrow d=(8)/(2)=4 \\ d=4 \end{gathered}`

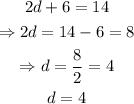
therefore, the value of d is d = 4.

We have now the explicit formula for the sequence:

`\begin{gathered} a_n=6_{}+4(n-1) \\ \end{gathered}`

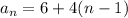
then, for the 20th term, we have to make n = 20 on the formula, and we get the following:/

`\begin{gathered} a_(20)=6+4(20-1)=6+4(19)=6+76=82 \\ \Rightarrow a_(20)=82 \end{gathered}`

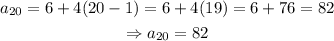
therefore, the 20th term is 82